When adding ones together would create a number larger than 10, bridging is a strategy that can be used. To perform bridging, a pupil must have good recall of the bonds for 10, be able to decompose single digits confidently and add single digits to 10.

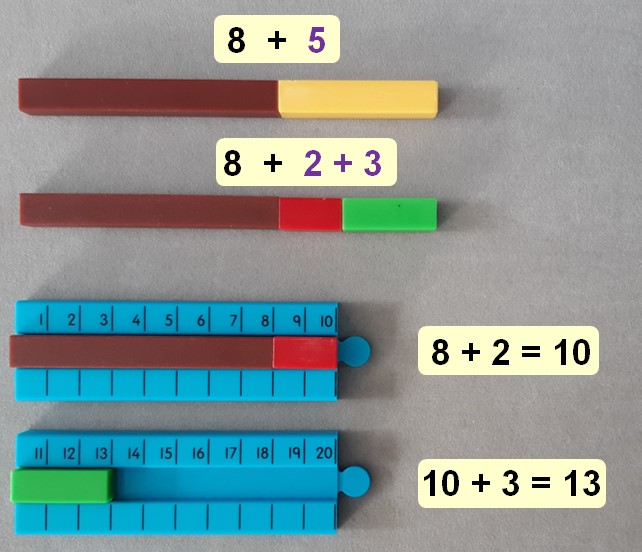
Adding two single digits can involve bridging across 10, in which we first add enough to make 10, then add the rest. Bridging is a useful strategy as 10 is an easy number to add to, and we can reach 10 using known facts, meaning that we don’t have to count in ones.

To add 8 + 5, we can look at the 8 and use number bonds for 10 to know that adding 2 more to the 8 would give us 10. Needing to add 5 altogether and having already added 2, there is 3 left to add onto the 10, giving a total of 13.

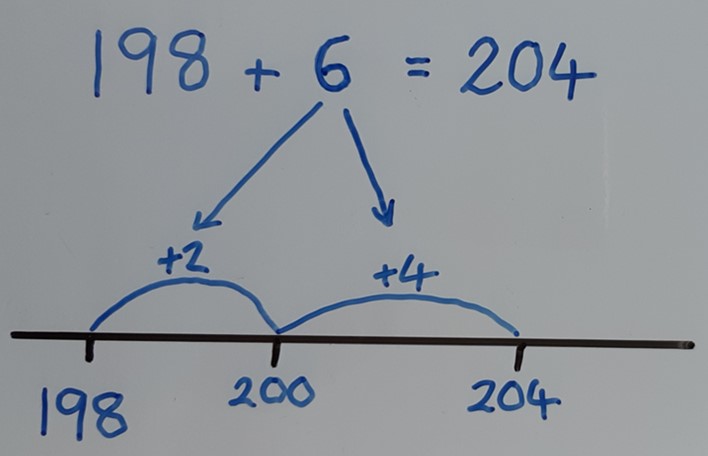
Bridging is a strategy that can also be applied to add across multiples of 10, 100 or 1000, applying the bonds for 10, 100 or 1000 as appropriate.